Helmert or affine transformation parameter editing and converting to inverse transformation.


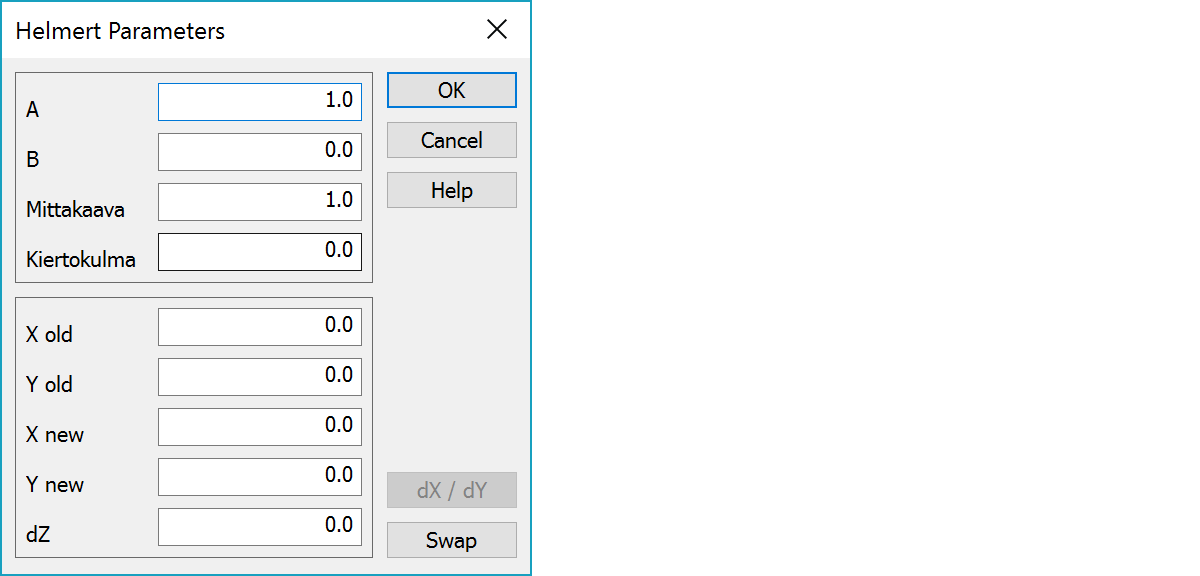
Parameters of the Helmert transformation. Editing A- and B-parameters changes automatically scale and rotation angle. Editing scale and rotation angle changes automatically A- and B-parameters.
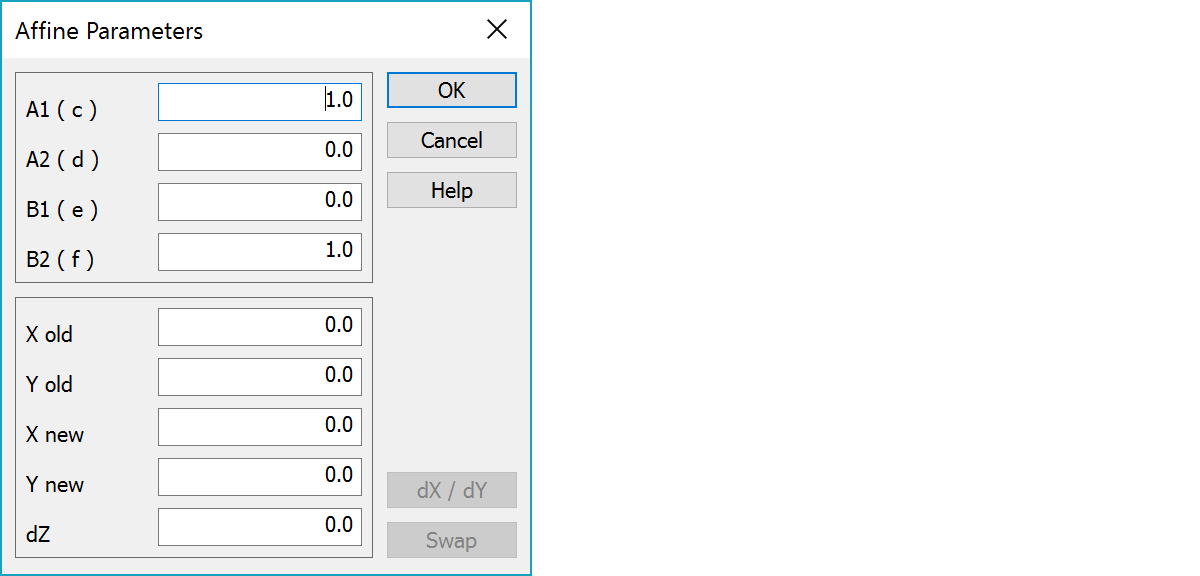
Parameters of the Affine transformation.
When using the center point method, there are coordinates of the center point of the old coordinate system. Otherwise these values are zeroes.
When using the center point method, there are coordinates of the center point of the new coordinate system. Otherwise these values are dx and dy values of the transformation.
In addition to normal two-dimensional Helmert-transformation, the height level can also be changed.
Converts weight center parameters to dX/dY translation parameters.
Inverts transformation. Handling of the XY values depends if the old coordinate system center coordinates were given. dZ values changes sign.
The parameters can be defined in a formula:
X = X0 + X * A - Y * B
Y = Y0 + X * B + Y * A
Be aware of the sign of B.
Below is an example from National Land Survey of Finland. Conversion from Helsinki City into KKJ.
P = PHelsinki - 21411.896
I = IHelsinki - 51725.460
PKkj = 6676543.079 + 0.9999286 * P + 0.0139389 * I
IKkj = 2554561.907 + 0.9999286 * I - 0.0139389 * P
resulting:
A = 0.9999276, B = -0.0139389
X old = 21411.896, Y old = 51725.460, X new = 6676543.079, Y new = 2554561.907
The parameters can be defined in a formula:
xx = a + cx + dy
yx = b + ex + fy
a = 47.9729266055
b = -2000051.8003553776
c = 0.9999976876
d = -0.0000122328
e = 0.0000109212
f = 0.9999911101
resulting:
A1 (c) = 0.9999976876, A2 (d) = -0.0000122328, B1 (e) = 0.0000109212, B2 (f) = 0.9999911101
X old = 0.0, Y old = 0.0, X new (a) = 47.9729266055, Y new (b) = -2000051.8003553776